
Design and analysis of algorithms are a fundamental topic in computer science and engineering education. Many algorithms courses include programming assignments to help students better understand the algorithms. Unfortunately, the use of traditional programming languages forces students to deal with details of data structures and supporting routines, rather than algorithm design. Python represents an algorithm-oriented language that has been sorely needed in education. The advantages of Python include its textbook-like syntax and interactivity that encourages experimentation. More importantly, we report our novel use of Python for representing aggregate data structures such as graphs and flow networks in a concise textual form, which not only encourages students to experiment with the algorithms but also dramatically cuts development time. These features have been implemented in a graduate level algorithms course with successful results.
Algorithms are the single most important toolbox for anyone who must solve problems by writing computer programs. Algorithms are used not only by computer scientists and computer engineers, but also by many in other engineering and science disciplines. As a result, algorithm courses are taken by not only computer majors as a requirement, but also by students from other majors.
While it is possible to study algorithms just by reading textbooks and doing problem sets, students often do not really learn the algorithms until they actually try implementing them. As a result, it is not uncommon for algorithm courses to include programming assignments. Textbooks that include programming as an integral part of algorithm education have also been authored to meet this demand [4]. Virtually all courses and textbooks so far have asked students to program in a traditional language such as C or C++, and recently Java has gained popularity [5]. The argument for using these languages is mainly a practical one: students are probably already proficient in these languages; even if they are not, learning these languages would give them a practical skill.
Unfortunately, experiences have shown that programming assignments in algorithm classes may not always be pedagogically beneficial. Even though most algorithms are a few lines to half a page long in the textbook, their implementation often requires hundreds of lines in C or Java. One reason is that these languages require declaration of global variables, local variables, and parameters before they can be used. Another reason, more importantly, is that many data structures such as lists, linked data structures, and specialized arrays must be designed and implemented to support the algorithm, and the complexity of these exercises grows rapidly when aggregate data structures such as graphs or flow networks are involved. In fact, most object-oriented programmers spend the majority of their effort in designing the classes and interfaces, and spend relatively little time filling in the code for the methods. As a result, these programming assignments will force students to spend much of their time practicing programming issues, rather than algorithm issues. Students who are not computer majors tend to be put at a severe disadvantage.
Some instructors attempted to alleviate this burden by giving students library routines for the data structures. However, there are still many problems that are inherent to these traditional languages, including input/output and reuse. For example, a library might provide an API for building a tree or a graph before invoking the algorithm with the data structure. Students must either hardwire their test case, which makes successive calls to add one node at a time to a graph, or read a description of the graph from a file. The former approach can be awkward, because the source code does not resemble the data structure, but the meaning is tied to the API. The latter approach, which uses a custom language to represent a graph, may be more concise, but it requires parsing routines, which can diminish reuse and expandability. For example, consider the case where we initially defined an unweighted graph but later want a weighted graph. It may be easy to create a subclass for the weighted extension, but we also need to change the parser to handle the weighted or unweighted case. But suppose we want to extend the weights again to a tuple, a string, or an arbitrary set: the parser must be changed each time.
Python addresses these problems and makes a compelling language for algorithms education. First, its indentation-based syntax is so similar to most textbooks that even students without much programming background have no trouble coding up algorithms just by following the book. Therefore, the popularity argument with other languages is moot, especially given the fact that its interactive mode encourages students to experiment with it without the long compilation cycle. Second, Python provides the fundamental data structures such as lists, tuples, and dictionaries that can be used directly by the algorithms. Even the more complex data structures such as trees and graphs can also be expressed in Python in a concise, human-readable form, without having to reinvent those data structures. For example, Section 5 will show a novel way of representing a weighted graph as a dictionary of vertices whose adjacency lists are represented by dictionaries of edge weights. There are several advantages: the test cases for the algorithms can be written directly in Python without having to call any data-structure-building API, and without having to rely on any custom parser. Moreover, it is infinitely extensible to arbitrary data types, as Python simply passes them along and does not interpret the data type until needed. At any time, the data structure can also be displayed in textual form that is readable to humans and by Python.
The rest of this paper reports our successful experience with deploying Python in a graduate level algorithms class. Our students have been not only receptive but also acquired a valuable tool to help them solve problems in their own field of study. The following sections illustrate how we teach algorithms in Python, in the same sequence as presented in class. We start with sorting algorithms and heapsort with priority queues to highlight memory management issues. Then, we use them to build binary trees and implement the Huffman compression algorithm. Finally, we show how Python can be used effectively for graph algorithms.
Most textbooks start with sorting as a way to introduce algorithms and complexity analysis. We use sorting algorithms to also introduce Python from the very first lesson. Our strategy is to display the algorithm side-by-side with Python code to show their similarity. We start with InsertionSort, which grows the sorted array one element at a time from the beginning of the array. Initially, A[1] (in text; A[0] in Python) is the only element in this subarray and is trivially sorted. Each iteration of the for-loop inserts the next new element into the sorted subarray so that the elements are sorted relative to each other; this is in contrast to BubbleSort, which puts a new element in its absolute sorted position per iteration.
Algorithm from textbook [1]Insertion-Sort(A)
1 for j <- 2 to length[A]
2 do key <- A[j]
3 i <- j - 1
4 while i > 0 and A[i] > key
5 do A[i+1] <- A[i]
6 i <- i - 1
7 A[i + 1] <- keyPython code
def InsertionSort(A):
for j in range(1, len(A)):
key = A[j]
i = j - 1
while (i >=0) and (A[i] > key):
A[i+1] = A[i]
i = i - 1
A[i+1] = key
Once students see the similarity, most of their fear of programming simply disappears. It also helps to demonstrate the interactive nature of Python. We use a computer projector and actually type in the program, which is only 8 lines long. The best part is, we can test out the algorithm by simply typing in the test case in the form of a list:
>>> x = [2,7,3,8,1] # create test case
>>> InsertionSort(x) # call routine
>>> x # look at result
[1, 2, 3, 7, 8]
In a sense, Python gives the textbook relevance because the algorithms presented in the textbook are no longer just pseudocode or steps of theoretical interest only; they can see how easy it is to actually execute the algorithms using data that they generate. In fact, we also show that the same code, without alteration, works just fine with other data types, including strings, tuples, etc. Sorting is a good starting example because not only do the constructs map directly without the complication with memory management (to be discussed later), but the parameter semantics also matches: scalars are passed by value, whereas arrays are passed by reference.
Our introduction continues with heap sort and priority queues. A heap is a data structure that represents a nearly balanced binary tree using an array A[1..n], where the left and right children of an element A[i] are located at A[2i], A[2i+1], respectively, and A[i] >= A[2i], A[2i+1]. HeapSort builds the sorted subarray from the back of the array towards the front one element at a time by extracting the largest element from the front of the heap. Initially the sorted portion is empty, and a call to BuildHeap turns A[1..n] into a heap. Since the heap part puts the largest element at A[1], in the first iteration we extract it and put it in A[n], which is its correct sorted position. The next iteration extracts the second largest element (from A[1] again) and puts it in A[n-1], etc, and it continues until all of A is sorted. Note that Heapify is called as part of each extraction step. This is because if we swap A[1] and A[h], then A[1..h-1] no longer satisfies the heap property, but since it is still "almost" a heap -- that is, all except the root position are still subheaps -- it can be fixed efficiently in O(lg h) time by calling Heapify without having to rebuild the heap in O(h) time.
One difference is that the algorithm in the textbook assumes 1-based array indices, whereas Python assumes 0-based arrays. To avoid errors due to index adjustment, we ask the students to simply pad their A[0] with None and use an array of size n+1 instead. The Python code is
def Parent(i): return i/2
def Left(i): return 2*i
def Right(i): return 2*i+1
def Heapify(A, i, n): # A is "almost a heap" (except root); fix it so all of A is a heap
l = Left(i)
r = Right(i)
if l <= n and A[l] > A[i]: largest = l
else: largest = i
if r <= n and A[r] > A[largest]:
largest = r
if largest != i:
A[i], A[largest] = A[largest], A[i]
Heapify(A, largest, n)
def HeapLength(A): return len(A)-1
def BuildHeap(A): # build a heap A from an unsorted array
n = HeapLength(A)
for i in range(n/2,0,-1):
Heapify(A,i,n)
def HeapSort(A): # use a heap to build sorted array from the end
BuildHeap(A)
HeapSize=HeapLength(A)
for i in range(HeapSize,1,-1):
A[1],A[i]=A[i],A[1] # largest element is a root of heap, put it at the end of array
HeapSize=HeapSize-1 # shrink heap size by 1 to get next largest element
Heapify(A,1,HeapSize)
Heaps and priority queues are closely related, since heaps can implement priority queues efficiently with O(lg n)-time insertion and extraction. One difference, though, is dynamic memory management: in heap sort, the size of the array remains the same, whereas in priority queues, the size of the queue grows and shrinks. We use this opportunity to introduce two constructs. First, we show that A.append() and A.pop() can be used to grow and shrink the list A, while len(A) returns the current length of the list. Second, in case of underflow (and overflow if desired), we show the students how to raise and catch an exception. These constructs might not be unique to Python, but Python makes it easy to experiment.
Once we have the priority queue, we enable students to quickly implement interesting algorithms, including Dijkstra's single-source shortest paths and Prim's min-spanning tree. Our next topic is greedy algorithms, and we ask the students to implement Huffman encoding in Python. To recall, the Huffman algorithm produces prefix-free, variable-length code words based on the frequency of each character. A frequently used letter will be encoded using a shorter bit string, whereas a less frequently used letter will be encoded using a longer bit string. The greedy algorithm uses a priority queue to extract two nodes (leaf or internal) with the lowest frequencies, allocates a new node whose weight is the sum of the two, and inserts the new node back into the priority queue. The algorithm terminates when the priority queue removes the last node, which becomes the root of the Huffman tree. The bit string for each letter can be produced by traversing the Huffman binary tree, where taking a left branch results in a `0', and a right branch results in a `1'.
For example, suppose our input character set with the associated frequencies is
The Huffman algorithm constructs a tree by repeatedly dequeuing two elements with the least frequencies, creating a new internal node whose frequency is equal to their sum, and enqueuing it in the priority queue. The result is a tree (Fig. 1) that defines the variable-length code for each character. The left branches are labeled 0, and right branches are labeled 1, and the Huffman code for a character is simply the string of path labels from the root to the leaf. For example, the encodings are

Since we already have the priority queue, what we are missing is a specialized binary tree. The requirements are
If we were to implement this with a traditional language like C or Java, we would have to teach students how to define a structure or a class with a field named weight; leaf nodes need a character field, while internal nodes require leftchild and rightchild fields. Because the priority queue must be able to compare them, it will be necessary to modify the priority queue to call the appropriate comparison method instead of using the built-in comparison operators, and both the leaves and internal nodes must either be in the same class or be subclasses of the same base class that implements the comparison method. Once defined, the student will want to able to check if they construct the Huffman tree correctly. However, no existing debugger has the knowledge to be able to automatically print the nodes together as a tree, and therefore the student has the burden of having to write the print routine, which may actually be rather tricky and be another major source of bugs. Similarly, for the students to specify the different test cases, they will either have to modify the hardwired data and recompile each time, or they will need to write additional parsing routines, which will be yet another source of errors.
A Python implementation can be done elegantly without having to write extra routines or defining a new class or a structure for the tree nodes. We ask students to represent binary trees using tuples in Python, in a spirit similar to Lisp:
The tree is constructed functionally with tuple creation, without having to use any tree node data structure, and there is no need to manipulate the left/right child pointers. Moreover, it is readily usable with the existing priority queue data structure, without any modification! This is because tuples can be compared in lexicographical order using the same comparison operators. This way, internal nodes and leaves can be compared, even though they encode different information. The difference between them is that the len() = 2 for a leaf, and = 3 for an internal node.
To recap, with a slightly creative way to use Python, we achieve the ultimate reuse of algorithms and data structures. It also enables the students to textually describe a tree in Python syntax that is as concise and extensible as possible, without having to use a specialized parser.
A graph is G(V,E), where V is a set of vertices, and E, as a subset of the cross product of V cross V, is a set of edges. A graph has multiple representations, and most algorithms assume either an adjacency list or an adjacency matrix representation. The former is good for sparse graphs where |E| is much closer to |V|, whereas the latter is good for dense graphs whose |E| is closer to |V|2.
To implement a graph in a traditional system programming language such as C or Java, one would first have to define data structures for the vertices, for the edges, and for the graph, which serves as a front-end to the creation and deletion of its vertices and edges. The design of such data structures can easily dominate the coding time and is not easily reusable, mainly because these data types must be designed as containers. Even though packages like LEDA [3] attempt to enhance reuse of object-oriented source code with C++ templates, they still require that the students adopt the entire package before they can start doing anything useful. Containers are often designed to circumvent the problems with strong, static typing, but doing so requires the reimplementation of dynamic type checking in end-user code. An even worse drawback is that the use of C-pointers or Java-references makes it awkward to view these objects. Even though a debugger can display these objects in some textual form, it either displays too much information or is not directly usable in the program.
Python offers many advantages as highlighted by the graph data structure. We use a very compact, dictionary-of-dictionaries (DD) implementation of the adjacency list representation of the graph. Basically a graph is represented as a Python dictionary, whose keys are the string names of the vertices, and each vertex name is mapped to its adjacency list. For example, consider the graph shown in Fig. 2:
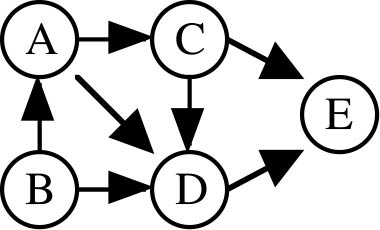
It can be represented with the following Python code
H = {'A': ['C', 'D'], 'B': ['D', 'A'], 'C': ['D', 'E'],
'D': ['E'], 'E': [] }
The above represents a simple, directed, unweighted graph. If a weighted graph such as Fig. 3 is required, then we can simply replace the lists of adjacency vertices with dictionaries that map the adjacent vertices to their weights:
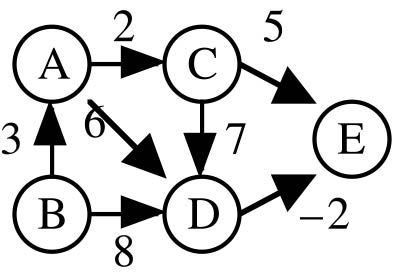
L = {'A': {'C':2, 'D':6}, 'B': {'D':8, 'A':3},
'C': {'D':7, 'E':5}, 'D': {'E':-2}, 'E': {}}
The list of vertices V is simply H.keys() or L.keys(). The adjacency list is H[v] for unweighted graphs, and L[v].keys() for weighted graphs. The edge weight w(u,v) is L[u][v]. To facilitate programming, we can wrap the implementation details inside an object.
class Graph:
def __init__(self, g):
self.g = g
def V(self):
return g.keys()
def Adj(self,v):
return self.g[v].keys()
def w(self,u,v):
return self.g[u][v]
We can create a graph object with G = Graph(L). The advantages with this approach include the compact textual format and extensibility. First, there is really no data structure to design. The textual representation of the graph is Python executable. The student can type in this structure interactively or in a text file without using any special graph editor. The data structure can be examined just by typing its name. It can then be cut/pasted to another Python interpreter window or to another Python program, without any syntactic modification.
More importantly, this representation is extremely extensible. Different algorithms make use of additional attributes, but they can be added as needed. For example, single-source shortest path algorithms or breadth-first/depth-first traversals require additional attributes such as the predecessor pointers. In Python, the algorithm can simply add the predecessor attribute to the graph object (as G.pred[v]), without having to define a subclass for each algorithm. These newly added attributes can also be examined and modified directly without requiring new routines.
As of this writing, we have offered the algorithm class twice with Python. Overall, the results have been very positive, although there is still room for improvement. This section discusses both aspects with anecdotes.
On the successful side of the story, most students appeared receptive to Python, and most of the 35-40 students from each class were able to successfully complete the programming assignments without much difficulty. At least one student became a Python fan and switched from C++ to Python for his own research work after this course. Currently he not only uses Jython and TkInter to script user interface widgets but also uses Python for sockets programming, multithreading, and scripting native C code. What was more encouraging was that several students who were not experienced programmers became quite good at Python by the end of the quarter. They successfully implemented the Edmonds-Karp's max-flow algorithm, which was not fully given in the textbook, and tested it with several examples in as little as one hour. Another student, also without much prior programming background, spent a greater part of his weekend on the same assignment, but was eventually successful after some hints from the instructor. He remarked that part of the difficulty was with the copy and parameter passing semantics in Python, but the main problem was that he had not really understood the E-K algorithm. Once he really understood it, then coding it up was actually very simple. The most encouraging part was that more than a few students wanted to implement the algorithms that were not assigned as homework problems. The students said they wanted to see the algorithms run and test their own understanding. These anecdotes all served to validate our prediction and confirmed the reasons we incorporated Python in the course in the first place.
Not all students had a smooth experience with Python, though. One common complaint was the lack of a good debugger. The author responded to the students by asking them to write small routines and to test them thoroughly before writing more code, instead of writing a large program and expecting it to work on the first try. However, not all students were convinced. The copy semantics of composite data structures such as lists, dictionaries, and objects also caused some confusion, though we plan to correct this issue by including their explanation as part of the reading assignment. In some cases, it turned out that some of the students with more experience with C++ or Java had more trouble adjusting to Python. Some felt uneasy with the idea of loose typing, while others had trouble thinking about vertices as just a string that could be used as a hash key to different attribute dictionaries; instead, they wanted to think about vertices as objects. A few students did not follow the instructions for the graph or the Huffman tree data structures as presented above, and they effectively wrote Java or C++ style code in Python syntax by defining many classes and subclasses. One such program listing for Huffman was over 12 pages long, even though most other students did it in about one page. As predicted, most of the 12 pages of code dealt with manipulating data structures and printing the pointer-connected data structures in a textually meaningful way. This was not really a problem with Python, and in fact it is motivating us to introduce Python earlier in the curriculum.
This paper reports our use of Python in an algorithms course in the past two years. As an algorithm-oriented language, Python enables our students to learn key concepts in algorithm design, instead of struggling with low-level, idiosyncratic features of conventional programming languages. The way Python handles data types represents a perfect match with the way textbooks present algorithms, and its interpretive nature encourages students to experiment with the language. Equally important is our novel use of data structures for trees and graphs, which are as compact as possible and yet human readable and is readily accepted by the Python interpreter. Graduate students who had little or no programming experience have been able to experiment with the algorithms at the level intended by the textbook, without being bogged down by many low-level programming issues.
We have adopted Python in not only our classrooms but also research projects as well, since research can benefit just as well from the same advantages. We are also encouraged by feedback from our former students who have adopted Python in their current work. We are currently revamping our undergraduate introductory programming series to include Python in a major way. As of this writing, this department just received the University's approval to replace C with Python in the first introductory programming class (ECE 12), starting Fall quarter 2002. We had to overcome some strong opposition from some non-computer engineering faculty members who had never heard of Python and were doubtful about our approach. We were criticized for trying to make programming "too soft" for engineering students, and we were asked "if C ain't broke, why fix it?" Our response was that we want to teach problem solving skills, not just programming, and we are confident that Python will be a much more effective way to introduce the fundamental concepts than C. The availability of CGI and graphics packages in Python through Jython and TkInter will also provide more compelling ideas for student projects than C or Java.